Huffman Coding in Python

I have wanted to tackle the Huffman Coding algorithm for some time and am finally able to get around to it. Huffman Coding is a compression algorithm used to decrease the number of bits used to store text. While there are several more complex and more efficient algorithms that exist, this one serves as a base and really helped programmers start entering the world of compression.

How it Works

Huffman Coding starts with a string. For example, let's use "Apple" as our string. The first step to this algorithm is to count the number of occurrences of each letter in your string. I am going to call this "frequency." In our example, every letter only appears once, except for "p," which appears twice.

With that information, we can now start creating a "node tree" that will allow us to get unique binary codes for each character. We start this process by grabbing the two least frequent letters and create a parent node above them that holds the sum of their frequencies. For example, let's choose "l" and "A" as they both only appear once. The node above them that we create contains the value "2," as that is the sum of the child nodes' frequencies. We then add the new node we created back into the system so we can sort it again. We continue this process until we come to something that looks similar to the following image:

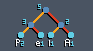
As you can see in this image, we have a root node at the top with a value of the total number of characters in our string. Below that node, we have connecting nodes that lead down to each individual character.

Using the Nodes to get the Codes

Now that we have our node tree set up, we will use it to get unique codes for all of the individual characters in our string. To do this, we will always start at the root node. When moving to the left, we will add a "1" to our code. If moving to the right, we will add a "0." Continue following the tree down until you reach a character. Now save that code with that character and repeat this process for all of the other characters.

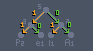
This will leave us with the following codes: A: 00, l: 01, e: 10, p: 11. Now, if we convert all of the characters in our string to their corresponding codes, we will get 0011110110. That value along with the node tree can be saved together to compress any file.

My Implementation

Below is the Python script that I wrote to simulate Huffman Coding. It takes an input value, encodes that value, and then also decodes the value it encoded.

codes = {}

def start_huffman_coding():
    global codes
    codes = {}

    text = input("Enter text to apply Huffman Coding to: ")
    root_node = create_nodes(text)
    assign_character_codes(root_node)

    encoded_text = "".join([codes[character] for character in text])
    print("Encoded text: ", encoded_text)
    decoded_text = decode_huffman_coded_text(encoded_text)
    print("Decoded text: ", decoded_text)

def decode_huffman_coded_text(encoded_text):
    reversed_codes = {value: key for key, value in codes.items()}

    decoded_text = ""
    current_code = ""
    for bit in encoded_text:
        current_code += bit
        if current_code in reversed_codes:
            decoded_text += reversed_codes[current_code]
            current_code = ""

    return decoded_text

def assign_character_codes(condensed_node):
    explore_node(condensed_node, "")

def explore_node(node, code):
    if node is None:
        return
    if node.character is not None:
        codes[node.character] = code
        return
    
    explore_node(node.left_node, code + "0")
    explore_node(node.right_node, code + "1")

def create_nodes(text):
    nodes = [Node(character, frequency) for character, frequency in get_frequencies(text).items()]

    while len(nodes) > 1:
        nodes.sort()
        left_node, right_node = nodes.pop(0), nodes.pop(0)
        parent_node = Node(None, left_node.frequency + right_node.frequency, left_node, right_node)
        nodes.append(parent_node)

    return nodes[0]
    
def get_frequencies(text):
    frequencies = {}
    for character in text:
        if character not in frequencies:
            frequencies[character] = 0
        frequencies[character] += 1
    return frequencies

class Node:
    def __init__(self, character, frequency, left_node = None, right_node = None):
        self.character = character
        self.frequency = frequency
        self.left_node = left_node
        self.right_node = right_node

    def __lt__(self, other):
        return self.frequency < other.frequency
    
    def __repr__(self):
        return f"Node({self.character}, {self.frequency})"
    
if __name__ == "__main__":
    start_huffman_coding()